Das gleichseitige Dreieck symbolisiert die zeit- und raumlose, göttliche Weise – die Bewegung (Dynamik). Sie verbindet (3) die in ihr enthaltenen Gegensätze (1+2). Möglich ist das, weil sie auf diese nicht willkürlich einwirkt sondern sie in „rechter“, d.h. in sich gegenseitig bewahrender Weise in Beziehung stellt. Jeder der beiden Pole begründet sich dabei als Ursache des anderen.

Mit anderen Worten: Jeder der Pole existiert durch den anderen und nicht durch dessen Vernichtung. Diese sich gegenseitig bewahrende Weise äußert sich in der geometrischen Gesetzmäßigkeit des Dreiecks: Das Dreieck besteht aus drei gleichen Prinzipien, den drei Winkeln. Der Winkel symbolisiert das Prinzip der Verbindung zweier Linien. Gemäß der Zweizahl begrenzt er und engt ein.[i]  Infolge der Dreizahl der Winkel entfalten sie jedoch eine Wirkung, die das Prinzip der Zweizahl der gegenseitigen Aufhebung und Vernichtungsangst enthebt und es stattdessen durch Addition erhöht. Durch das ganzheitliche Zusammenwirken der Teile entsteht in jedem beliebigen Dreieck eine Winkelsumme von 180° (3x 60°= 180°). Ihre Bedeutung liegt in der nun möglichen, anderen Sichtweise auf sie. Aus der Sicht der Zweiheit der Gegenpole ist sie zugleich die Summe zweier rechter Winkel (2×90°=180°)! Mit anderen Worten: Sowohl aus der Sicht der Dreiheit als auch aus der Sicht der Zweiheit wird stets ein größeres Ganzes, die Einheit offenbart. Jedes Dreieck enthält also die verdeckte Information, dass durch seine Wirkung ein Gegensatz erlöst wird. Die beiden gegensätzlichen Sichten einer Polarität entfalten im Dreieck jede für sich ein rechtes Verhältnis (90°) zur jeweils anderen.

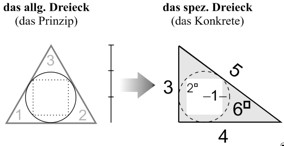
Das in jedem Dreieck wirkende, archetypische Gesetz drückt sich in der Vielzahl der möglichen Dreiecke unterschiedlich aus. Von besonderem Interesse ist aber das Dreieck, das einen nächsten Entwicklungsschritt anzeigt und die dem Archetyp entsprechende Dreizahl nicht nur sichtbar werden lässt sondern sie darüber hinaus auch noch mit der ihr folgenden Vierzahl in ein rechtes Verhältnis setzt. Das leistet das rechtwinklige Dreieck mit den Katheten der Länge 3 und 4. Wir kennen es als das pythagoreische Dreieck 3-4-5, das zudem auch noch die Fünf- und die Sechszahl sichtbar werden lässt.

[i] Beachte die etymologische Verbindung vom lateinischen „angulus“ (Winkel) und Enge oder Angst.