Eine Sammlung zum Thema Zahlen von Dr. Michael Stelzner
Die Zahlen und ihre Grenzen
(Zahl + Grenze.docx)
Der Wiener Mathematiker Kurt Gödel hat gezeigt, dass die Mathematik unvollkommen und nicht in der Lage ist, aus sich heraus ihre eigene Konsistenz zu beweisen. Um zu erklären, was Mathematik ist und weshalb sie funktioniert, muss man notwendigerweise aus der Mathematik herausgehen. Aus mathematischer Sicht bedeutet es, aus den mathematischen Algorithmen und ihrer Interpretation durch das nur Rechnen herauszugehen. Mathematische Algorithmen sind mächtige Werkzeuge, doch scheitern sie an den zwei größten Wesenheiten, dem Ganzen und der Grenze und ihrem Verhältnis.
Die Mathematik ist nicht das heilige Reich der absoluten Perfektion für das sie bis zu den Beweisen von Gödel gehalten wurde. Sie kann es nicht sein, weil ihre Bausteine, die zählenden Zahlen die Existenz von Qualitäten ausschließen und deshalb selbst nicht perfekt sind. Die Zahlen sind eine Sprache und wie jede Sprache sind sie etwas Konkretes, Manifestes und somit (Be-)Greifbares, auch wenn dieses hier in einer besonders subtilen Form vorliegt. Jedes Konkrete bringt immer auf seine Weise das Ganze und seine Grenze zum Klingen. Die Zahl führt uns diese natürliche Eigenschaft des Konkreten erstrangig vor Augen. Doch es gilt auch: Selbst wenn wir die quantitativ-zählende Seite der Zahl durch ihre qualitativ-erzählende Seite ergänzen, so können wir möglicherweise ihre mathematischen Fähigkeiten erklären, doch bleibt sie eine Zahl und damit weiterhin ein Konkretes. Die Ergänzung macht sie vollkommener und in ihrem Konkretsein subtiler. Das Konkrete nähert sich asymptotisch an das Geistige an, bleibt aber von diesem immer unterschieden. Am Ende steht vor unserem Auge nach wie vor die Urpolarität des Ganzen und der Grenze, der Einheit (1) und der Polarität (2).
Wir können verstehen, weshalb uns die Zahlen die großen Zusammenhänge erklären. Sie zeigen uns sogar die zwei großen Endpunkte, das Ganze und die Grenze auf. Der nächste und größte Schritt aber ist die Erkenntnis des Subjektes über das, was hier eigentlich geschieht. Das Subjekt, dass diesen letzten und höchsten, polaren Zusammenhang erkennt und über ihn die Einsicht im wahrsten Wortsinn entwickelt, erhebt sich schauend über die Dinge.
Die Zahlen führen uns sehr weit, aber sie führen uns nicht zu dem einen letzten Endpunkt. Hier behält Aristoteles mit seiner Kritik an den Zahlen ebenso recht wie Platon, der den Ideen mit den Zahlen ein Gesicht gibt. Die Zahlen bilden die Grenze und zeigen den Horizont auf. Mehr nicht. Das wirkliche Geheimnis liegt darin, nicht über die Grenze gehen zu wollen. Das ist das eigentliche Geheimnis des Moses. Auch Moses stand an der Grenze und durfte, konnte und wollte sie nicht überschreiten. Und dennoch und gerade dadurch ging er zu Gott ein. Das ist das wahre Geheimnis des Moses . So soll seine Geschichte, so soll seine Botschaft verstanden werden.
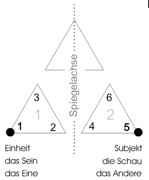
Der Mensch (5) – ein Spiegelbild der Gottheit (1)