Eine Sammlung zum Thema Zahlen von Dr. Michael Stelzner
PLATON - die Ideen und die Dreiecke
(Platon+Dreiecke.docx)
Inhalt
- Die Ideen
1.1 Die ungeschriebene Lehre – die Prinzipien oder die eigentliche Metaphysik
1.2 Die Zahlenkunst und die ungeschriebene Kernlehre
- Das Wiedererinnern alias das Selbstentdecken der Lehre von den Prinzipien
2.1 Die vier Wegweiser
2.1.1 Die Zahlen und die Zahlenkunst
2.1.2 Das Besondere – die Zahl 3
2.1.3 Die Dialektik – der sprachliche Zugang zur Metaphysik
2.1.4 Die Geometrie – der bildliche Zugang zur Metaphysik Platons
- Das Dreieck
3.1 Das Sierpinski-Dreieck
3.2 Das Pascal’sche Dreieck
3.3 Das Zahlendreieck (n. Stelzner)
- Die zwei Sichtweisen oder das Geist-Materie-Problem, Platon vs. Aristoteles
1.1 Das pythagoreische Dreieck – ein geometrisches Gleichnis
1.2 Die Ordnung der geometrischen Muster und die Ordnung der Philosophien
1.3 Aristoteles und die Konzentration auf das Objekt.
- Die Ideen
Nach Platon stellen nicht die Objekte der Sinneswelt die eigentliche Wirklichkeit dar, sondern allgemeine urbildhafte Ideen. Diese Ideen sind nicht nur Vorstellungen im menschlichen Geist, sondern haben eine objektive, metaphysische Realität. Für Platon existieren sie -wörtlich übersetzt – „über“ den sinnlich wahrnehmbaren Objekten, welche nur die Abbilder dieser Urbilder sind.
Platon selbst verwendete für diese Urbilder eine Vielzahl von Ausdrücken. Die bekanntesten Begriffe waren die bereits o.g. „idea“ oder „eídos“, welche unmittelbar mit „Idee“ wiedergegeben werden können und schließlich auch zum Begriff der Ideenlehre führte. Doch verwendete Platon für diese Urbilder auch andere Begriffe wie beispielsweise Gestalt (morphḗ), Gattung (génos), Muster (parádeigma) oder einfach Bild (eikōn). Die bekannten und von C. G. Jung aufgegriffenen und von da an weiter verwendeten Ausdrücke „Archetyp“ oder „urbildhaftes Muster“ (species archetypa) hingegen entstammen spätantiken Übersetzungen und Kommentaren der Dialoge Platons.
Obwohl erst durch Platon die Bezeichnung Idee bekannt und verbreitet wurde, existierte der Inhalt jenes Begriffs offenbar schon lange vor Platon bei den sogenannten Vorsokratikern. Das jedenfalls berichtet Augustinus und fügte selbst weitere Bezeichnungen hinzu. So gab er jenen gleichen Inhalt u.a. mit den lateinischen Lexemen „forma“ und „species“ wieder. Besonders aufschlussreich ist es, dass Augustinus den Ideenbegriff auch mit „ratio“ übersetzte, das eigentlich dem griechischen Wort „logos“ entspricht.[i] Dadurch rückt Augustinus „Christus als Logos“ (s. Joh 1,1) in die unmittelbare Nähe der Ideenlehre Platons oder setzt sie sogar gleich.
Für Platon waren die „über“ der Welt stehenden Ideen und Prinzipien von der „Zahlenkunst“, wie er es nannte, nicht zu trennen – im Gegenteil. Die Zahlen verbinden die Welt der Ideen mit der konkreten Welt der Dinge. So wie die Mathematik alle Bereiche der Welt durchdringt und daher auf ihre weitgehende Universalität aufmerksam macht, scheinen ihrerseits die allgemein urbildhaften Ideen in den mathematischen Gestalten nicht nur in besonderer Weise hervorzutreten sondern darüber hinaus wie keine anderen Gestalten dazu geeignet zu sein, die Ordnung der Ideen überhaupt zu erkennen. Durch die Einsicht in den Ideencharakter mathematischer Objekte mittels der Zahlen kann der Mensch die Ordnung allen Seins durchschauen – so Platon.[ii]
1.1 Die ungeschriebene Lehre – die Prinzipien oder die eigentliche Metaphysik
Die platonischen Dialoge brillieren durch eine besondere Klarheit und lassen eine regieführende Ordnung erahnen. Sie führen uns jedoch die behaupteten Ideen als Ganzes nicht systematisch und nachvollziehbar vor. Gleichwohl wendet sie Platon in seinen Dialogen praktisch an. Was wir sehen, ist gewissermaßen nur die Oberfläche der tieferliegenden System- und Prinzipienlehre. Uns interessiert jedoch nicht weniger als die Kernlehre selbst. Wir wissen von ihrer Existenz durch Aristoteles, denn der berichtet in seiner „Physik“[iii] ausdrücklich von einer „ágrapha dógmata“, einer „ungeschriebene Lehre“, die, so Aristoteles, nur im mündlichen Unterricht innerhalb der Akademie weitergegeben wurde.
Der bewusste Verzicht auf eine schriftliche Fixierung der Prinzipienlehre war ganz sicher nicht geleitet vom Wunsch einer Geheimhaltung, denn Platon hatte höchstes Interesse am Erhalt des Wissens. Im Dialog Phaidros begründet Platon denn auch ausführlich, weshalb die Schrift nicht geeignet sei, „Wertvolleres“ (timiōtera) zu vermitteln.[iv] So bleibt die Frage, wo wir heute nach der eigentlichen Lehre suchen müssen und wie wir sie möglicherweise rekonstruieren können?
1.2 Die Zahlenkunst und die ungeschriebene Kernlehre
Es gibt kaum ein philosophisches Grundthema, das Platon in seinen Dialogen nicht aufgegriffen oder behandelt hat. Doch ein Lehrfach bezeichnet er als ein „besonders feines Fach“, weil es, wie er es ausdrückte, „die Seele offenbar nötigt auf dem Wege des reinen Denkens sich der reinen Wahrheit zu nähern“. Er bezeichnete es als die Zahlenkunst. Unter der ist aber nicht, wie man es gemeinhin annimmt, die sogenannte Rechenkunst „wie bei Kaufleuten und Krämern“[v], zu verstehen. Die Platonischen Zahlen sind metaphysische und doch gestalthafte, sogenannte „eidetische“ Zahlen[vi], welche durch ihr Wesen von Qualitäten berichten und mit der herkömmlichen Zählkunst vor allem durch ihre strenge Ordnungsfolge korrespondieren und verbunden sind. Die Identität von Idee und Zahl lässt die Ideen besonders an ihren typischen geometrischen Eigenschaften erkennen. Das Besondere liegt dabei nicht nur im jeweils aufscheinenden Qualitätsmerkmal allein. Die so erkannten Ideen sind vor allem nicht beziehungslos. Sie bilden durch die hierarchische Ordnung der Zahlen wie diese eine klar erkennbare Ordnung der Ideen ab. Durch die Zahlenfolge können wir auch die Ideen, die sich unserem Geist sukzessive entfalten, verstehen und ordnen. Dabei gibt sich unserem Geist allerdings nicht allein eine ausschließlich lineare Ordnung der Ideen kund, wie sie uns das Bild des Zahlenstrahles vorgibt. Eine solche dient nur einer ersten Orientierung. Nach diesem linearen Muster wäre jede Idee auf eine konkrete Zahl zu reduzieren. Das aber macht die Prinzipienlehre durch das ihr innewohnende triadische Muster nur bedingt und das macht es auch so schwer, sie schriftlich dingfest zu machen. Würden wir ihre Aussagen nur linear verstehen, würden wir sie missverstehen. Die Linearität der Zahlenreihe ist ein anfängliches Hilfsmittel, allerdings ein überaus wichtiges. Ein anderes und ebenso gewichtiges ist die Triade, das Zusammenspiel der ersten drei Qualitäten: (1) „Einheit“, (2) Polarität und der diese beiden verbindenden (3) Funktion. Das Wissen, dass die Zahlen, ihre Linearität und die Triade den Rahmen der Lehre bilden, ist, wie wir sehen werden, ein geeigneter Anfang zur Rekonstruktion der Prinzipienlehre.
- Das Wiedererinnern alias das Selbstentdecken der Lehre von den Prinzipien
Die Philosophiegeschichte zeigt, dass jede Suche nach einer verbindlichen Metaphysik auf die eine oder andere Weise zu Platon führt und damit zur sogenannten Ideenlehre. Auch wissen wir, dass Platon die Ideenlehre mit der sogenannten Zahlenlehre („Zahlenkunst“) gleichstellte. Selbst wenn wir ihre unmittelbare, systematische Darlegung vermissen, so wissen wir doch, dass es sich dabei um ein klar erkennbares Ordnungssystem handelt und dass die „Anamnesis“, die sogenannte Wiedererinnerung die zentrale Rolle im Erkenntnisprozess spielt. Erkennen bedeutet nach Platon, sich wiedererinnern an das, was in jedem bereits als Ordnung persé vorhanden ist. Die Anamnesis macht eine unmittelbare, systematische Darlegung der Ordnungslehre überflüssig. Strenggenommen widerspricht sie ihr sogar: Am Ende geht es darum, das Wesen des Bewusstseins zu lüften und das hat einen dualen Charakter. Es setzt die Einheit von Schau und Handlung voraus -mit anderen Worten: die verbindliche Handlung. Wer sie aufzuheben versucht, der wirkt der Bewusstseinsbildung regelrecht entgegen.
Das Argument der Anamnesis wird zum Prüfstein der Wahrhaftigkeit und erklärt die scheinbare Unvollständigkeit der Werke Platons durch das Fehlen einer unmittelbaren Prinzipienlehre. Wenn Platon höchstes Interesse am Erhalt des Akademie-Wissens hatte, aber dennoch auf dessen direkte Verschriftlichung verzichtete, ihm zugleich aber die Gefahr und Wahrscheinlichkeit bewusst war, dass mündliche Überlieferungen verloren gehen oder verfälscht werden würden, so muss er auf eine ganz andere Weise für die Bewahrung des Wissens gesorgt haben. Der Gedanke ist so einfach wie genial: Nachfolgenden Generationen muss es möglich sein, das wahrhaftig erstrebte Wissen mit Hilfe seiner Texte selbst zu rekonstruieren.
Die richtige und effektivste Weise der Wissensvermittlung besteht in der Methode, die uns Platon immer wieder und ausführlich vorgeführt hat und die wir die „Hebammenmethode“ nennen. Es ist ein Dialog bei dem der Einzuweihende sich durch eigene Anstrengung das begehrte Wissen selbst erarbeitet. Man muss ihm nur – wie bei der dialektischen Methode in Platons Dialogen – die rechten Rahmenbedingungen und Parameter vorgeben. Diese sind die überlieferten Texte. In Verbindung mit der von Platon ausführlich dargelegten Wiedererinnerung lässt sich das Wissen Stück für Stück, Archetyp für Archetyp herauskristallisieren. Das Geniale an der Methode ist, dass sie ihre Feuerprobe einschließt. Platon hat vollends darauf vertraut, dass sie funktioniert. Sie kann es nur, wenn die Prinzipienlehre auch wirklich eine Archetypenlehre, d.h. eine universell wirkende ist.
2.1 Die vier Wegweiser
Eine wirkliche Universallehre schließt kein Wissengebiet aus. Der Entdecker einer Metaphysik, die ihren Namen vollumfänglich gerecht wird, kann darauf vertrauen, dass sie zu allen Zeiten nachentdeckt werden kann, sofern die wichtigsten Eckpfeiler einmal gesetzt wurden. Platons Werke liefern sie uns:
- die Zahlen (das Ganze)
- die „überragende“ Zahl 3 (das Andere, Zweite, Besonderes wirkt)
- die Dialektik, die praktische Umsetzung (die Funktion und Wirkung)
- die Geometrie (das manifestierte Bild vom Ganzen)
Die Zahlen (siehe 1) und die Geometrie (siehe 4) haben eine unmittelbare Beziehung. So, wie die Zahl 1 der Ursprung aller Zahlen ist, so ist die Geometrie der Ursprung aller Erscheinungen. Die Zahlen und die Geometrie verweisen wie kein Anderes auf das Ganze und Platon ging es um die Schau des Ganzen. Spätantike Autoren berichten, in Platons Akademie habe es eine Inschrift gegeben, die jedem der Geometrie Unkundigen den Eintritt untersagte. Auch wenn das konkret nicht so gewesen sein sollte, so beschreibt es doch, welche hohe Bedeutung der Geometrie in der Akademie zukam. Die Werke Platons bezeugen das. Man dachte geometrisch. Die dreidimensionalen, allseitig symmetrischen Körper, die wir heute noch mit den Namen Platon verbinden, standen dabei nur am Ende von weitreichenden, geometrischen Überlegungen.
2.1.1 Die Zahlen und die Zahlenkunst: So wie die Zahlen und die Geometrie nur Ideale sind und beispielsweise in Punkt, Linie, Kreis, Dreieck, Quadrat etc. zur Anschauung kommen und sich auf diese Weise über die kleinen und großen Unzulänglichkeiten des allzu Konkreten und Sinnlichen erheben, so erhebt auch Platon seine Philosophie über das unvollkommene, sinnliche Leben und folgt nur „idealen Objekten“, den sogenannten Ideen. Wo anders heraus sollten solche Ideen erwachsen als aus den Idealen von Zahl und Geometrie? Die Zahl symbolisiert das Ordnungsprinzip schlechthin und die Geometrie bringt es in ihren idealen Formen zur Anschauung.
Unter der Zahlenkunst versteht Platon eine „philosophische Denkart“ und ganz und gar nicht die profane Rechenkunst. Der steht er sogar sehr kritisch gegenüber, weil sie eine Kraft ist, welche die Seele „verkehrterweise anstatt nach oben, nach unten zieht“.[vii]
„Es obliegt uns also dies Fach (die Zahlenkunst!) zum gesetzlichen Lehrfach zu machen und diejenigen, die künftig im Staate der höchsten Amtsgewalt teilhaftig sein sollen, zu veranlassen sich der ZAHLENKUNST zuzuwenden und sich mit ihr zu befassen nicht etwa bloß in laienhafter Weise, sondern bis sie durch reine Vernunfttätigkeit zur Anschauung der wahren Natur der Zahlen gelangt sind, eine Art der Behandlung, die nichts gemein hat mit Kaufen und Verkaufen wie bei Kaufleuten und Krämern, sondern die auf den Krieg abzielt sowie darauf, der Seele die Umkehr aus dem Werden zu Wahrheit und Sein zu erleichtern.“
„ … was allen Künsten und Forschungen und Wissenschaften unentbehrlich ist, und was denn jeder mit als Erstes erlernen muss. diese ganz bescheidene Weisheit: die richtige Kenntnis der Eins, der Zwei und der Drei.“ (Platons Staat, siebentes Buch S.281)
2.1.2 Das Besondere – die Zahl 3: Platon legt großen Wert darauf, zu definieren, was unter der Zahlenkunst zu verstehen ist, um sie deutlich von der Rechenkunst „der Kaufleute und Krämer“ zu unterscheiden. Das aber genügt ihm nicht. Er hebt unter der nicht endenden Reihe der Zahlen, welche alle die Zahlenkunst ins Bild setzen, die Zahl Drei explizit hervor: „ … die Eins, die Zwei und die Drei“. Das ist keine Redephrase. Platon stellt die drei ersten Zahlen als eine Ganzheit von höchster Bedeutung vor. Sie ist der Schlüssel zu aller Erkenntnis. Die Aussage ist kein bloßes Theoretikum. Platon wendet sie an und setzt sie bei der Abfassung seiner Werke praktisch um. Wie hätte er auch auf die ungeheure Mächtigkeit einer solchen Universallehre verzichten können, wenn doch gerade ihr Wirken das Neue und Wunderbare dem bewussten Geist entlockt?
2.1.3 Die Dialektik – der sprachliche Zugang zur Metaphysik
Platons Art der Vermittlung ist die sogenannte „Hebammenkunst“. Sie besteht in den Dialogen seiner Figuren. In der Anwendung der dialektischen Methode erfüllen sie das Bewegungsprinzip der Dreizahl. Alle so entwickelten Erkenntnisse werden in einem Dreierschritt von (1) These, (2) Gegenthese und die sie (3) verbindende Schlussfolgerung erarbeitet. Die von Platon vorgeführte dialektische Methode ist nichts anderes als die Anwendung „der Eins, der Zwei und der Drei“ als „philosophische Denkart“.[viii] Durch ihr Wirken (3) wird ein Viertes (4) manifestiert, das zu der ihr vorangehenden Dreizahl nun erneut deutlich unterschieden werden kann, denn es ist zu ihr etwas völlig Neues. Es ist ein „Wunderbares“, da in ihm These und Antithese eines werden. Die Unterscheidung zwischen der ursprünglichen „geistigen“ Drei und dem nun „substantiell-manifesten“ Vierten kann auf rechte Weise nur – wie es das pythagoreische Dreieck zur Anschauung bringt – durch ein zu diesen wiederum Drittes wahrgenommen werden. Das ist der ihnen gegenüberstehende und sie verbindende, bewusste Geist – das Bewusstsein (5). Es ist in der Abfolge der ersten drei Ideen und der aus ihnen heraus manifestierten Vielzahl der Archetypen (4) ein Fünftes (5). Hinter dieser so von Platon ausgeführten Metaphysik in Form der ersten fünf „eidetischen“ Zahlen verbirgt sich die Geometrie des pythagoreischen Dreiecks der Seitenlängen 3, 4, und 5. In seiner Figur liegt die Antwort auf die Beziehung von Geist (3) und Materie (4), auf welche die scheinbar unterschiedlichen Philosophien von Platon (Geist / 3) und Aristoteles (Substanz / 4) aufbauen.
2.1.4. Die Geometrie – der bildliche Zugang zur Metaphysik Platons
Die Metaphysik, wie sie uns Platon vorführt, ist auf verschiende Weisen zugänglich. Den direkten Zugang bietet das theoretische Erschließen der Qualitäten der Zahlen. Ein anderer Zugang ist der sprachlich-didaktische, wie ihn Platon in der dialektische Methode vorführt. Ein wieder anderer ist der bildlich-geometrische Zugang. Er ist besonders anspruchsvoll aber zugleich der Königsweg zur Metaphysik, da er augenscheinlich Theorie und Praxis verbindet. Der bildlich-geometrische Zugang ist der über geometrische Gleichnisse. In ihnen werden die Zahlen sowohl in ihrer Qualität als auch in ihrer linearen Folge zusammen betrachtet und über das Spezielle der Dreizahl in der Geometrie in Beziehung gebracht.
Die Zahlen zählen und erzählen. Ihre Existenz ist eine grundlegende. Über sie stellt sich die Welt uns vor und durch sie erfassen wir die Welt. Die Zahlen existierten schon vor dem organischen Leben. Die Ordnung des Periodensystems der Elemente, das streng der Ordnung der Zahlen folgt, und die Quantenphysik, die uns zeigt, dass alle Existenzen grundsätzlich mit den ganzen Zahlen einhergehen, zeigen uns das.
Ebenso grundlegend wie die Zahlen im allgemeinen sind, nimmt unter ihnen, sobald wir die Welt hinterfragen, wiederum die Zahl Drei ein. Hinterfragen wir irgendeinen Vorgang, so drängt sich die Zahl Drei uns immer wieder auf. Selbst wenn wir wie Heraklit mit seinem bekannten „alles fließt“ (pante rhei) oder Aristoteles mit seiner Frage nach einer „ersten Bewegung“ alles auf das einfache Bewegungsprinzip zurückführen, so stellen wir fest, dass auch das durch die Zahl Drei beschrieben wird.
Die Zahl Drei und somit auch deren geometrische Form, das Dreieck haben in unserer konkreten Welt ganz offensichtlich eine besondere Geltung, denn sie prägen alle erdenklichen Erscheinungen der Schöpfung. Ohne sie, auch die grundlegende Triade genannt, ist Welt nicht denkbar. Wenn es ein Schöpfungsprinzip gibt, dann verbirgt es sich in dieser Dreiheit.
- Das Dreieck
Im Bemühen Ordnung zu erkennen dient unsere besondere Aufmerksamkeit dem Zusammenhang der Phänomene Dreieck und Zahl. Man kann ihre Verbindung auf verschiedene Weise betrachten. Eine aber bietet sich besonders an, denn: Einerseits ist das Phänomen der Zahl die Basis unserer Vorstellung von Linearität und Ordnung und andererseits müssen wir aus den vorgenannten Gründen das Ordnungsprinzip anhand der Dreizahl erhellen. Das verlangt, dass wir den Zahlenstrahl mit dem Dreieck direkt verbinden. Das Ergebnis ist ein fortlaufend wachsendes Dreieckmuster auf dem die Zahlen in ihrer natürlichen Folge abgetragen sind. Ich nenne dieses Gebilde einfach das „Zahlendreieck“. Es wird seinen Nutzen schnell zeigen, denn durch die entstehenden Beziehungen der einzelnen Zahlen untereinander werden deren verborgenen Qualitäten weitgehend erkennbar.
Bevor ich mich dem von mir vorgestellten Zahlendreieck® zuwende, möchte ich zwei andere Dreiecke vorstellen, in denen ebenso Zahlen systematisch angeordnet sind und in denen auch die besondere Beziehung zwischen Dreieck und Zahl sichtbar werden. Es handelt sich um das allgemein bekannte Sierpinski-Dreieck und um das über die Mathematik wohl noch bedeutender erscheindende Pascal’sche Dreieck. Wer sich mit beiden Dreiecke beschäftigt, der wird an der besonderen und grundsätzlichen Beziehung von Zahl und Dreieck nicht mehr zweifeln. Aus dieser Einsicht heraus entstand auch das o.g. Zahlendreieck.
3.1 Das Sierpinski-Dreieck
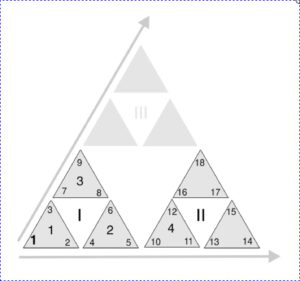
Betrachtet man ein Dreieck unter dem Aspekt seines eigenen Wesens, d.h. drittelt man es, so entstehen drei gleichgroße Einzeldreiecke. Das Gesamtgebilde schließt zusätzlich ein viertes Dreieck gleicher Größe ein. Das Vierte bildet nicht nur den Mittelpunkt. Es berichtet auch noch vom Prinzip des Gegensatzes, denn es weist entgegen den anderen Dreiecken, einschließlich des großen Ausgangsdreiecks, nach unten.
Den Vorgang der Teilung kann man unendlich fortführen, indem man jedes der 3 Teilungsdreiecke wiederum so behandelt wie ursprünglich das Ausgangsdreieck. Das so enstehende Gebilde ist ein Fraktal. Die jeweils mittigen, vierten Dreiecke sind aus der substanziellen Sicht des Fraktals Leerstellen und gehören aus mathematischer Sicht nicht zum Fraktal selbst. Ohne sie könnte allerdings das Ganze in der Gestalt des Fraktals nicht zur Erscheinung kommen!

Im Sierpinski-Dreieck sind keine Zahlen abgetragen, wie das beispielsweise im Pascal’schen Dreieck und im Zahlendreieck der Fall ist. Dennoch berichtet uns das Dreieck allein über seine Gestalt von den ersten vier Zahlen der Zahlenreihe und von deren natürlichen Beziehungen:
- Das Gebilde ist ein GANZES und EINHEITLICHES. Seine Gesamtstruktur, Größe und Umfang sind konstant.
- Die TEILE des Ganzen sind das Abbild des Einen und Ganzen. Sie bringen es über die Triade zur Anschauung.
- Über die Zahlen 1, 2, und 3 entfaltet sich eine FUNKTION, eine fraktale DYNAMIK welche eine systematische, innere und unbegrenzte Dreigliederung hervorbringt. Möglich wird sie, weil das, was geschieht, in Hinblick auf die grundlegende, einheitliche Gesamtfigur geschieht.
- Das sich manifestierende Gesamtgebilde basiert zum einen auf einer Drei-Einheit und es ist zum anderen untrennbar mit einem Vierten verbunden – dem vierten, mittleren Dreieck. Jenes Vierte bildet das Zentrum und somit den neuen Kern des Ganzen. Der aber drückt seinem Wesen nach etwas völlig Anderes aus als die ihm „vorausliegende“ Drei-Einheit (1-2-3). Das Vierte ist nicht nur das jeweils neue Zentrum. Es ist auch bezüglich der Substanzfrage und bezüglich der Ausrichtung und somit seiner Wirkrichtung ein anderes.
Im Sierpinski-Dreieck begegnet uns die Spannung (Polarität) zwischen der Dreiheit und der Vierheit. Sie wird sich später bei der Besprechung des Zahlendreiecks als die Urspannung zwischen Geist (3) und Substanz (4), alias Funktion (3) und Materie (4) zu erkennen geben. Jene Spannung konstituiert das Bewusstsein (5).
Das Sierpinski-Dreieck vereint also etwas, das aus einfacher Sicht eigentlich einen Gegensatz bildet – Geist und Substanz. Das einfache Denken ist ein lineares. Es bewegt sich entlang von Linien, ähnlich dem Zahlenstrahl, der uns zum Muster von Ordnung wurde. Sobald zu dieser Linienhaftigkeit ein Anderes, eine neue Dimension hinzutritt – hier die Fläche -, wird unsere Ordnung in Frage gestellt. Das Sierpinski-Dreieck macht uns das neben dem o.g. Aspekten auch noch auf eine weitere Weise deutlich: Das Fraktal entwickelt sich nach innen in die Tiefe der Gestalt. Dabei bleibt das Ausgangsdreieck von Größe und Umfang gleich groß. Nach der euklidschen Geometrie und ihrer linearen Interpretation verhalten sich Umfang und Fläche einer Gestalt jedoch proportional. Steigt die Fläche, so steigt auch der Umfang der Gestalt. Beim Sierpinski-Dreieck gilt das allein für das Ganze, jedoch nicht mehr, wenn wir auch seine fraktalen Eigenschaften berücksichtigen. Das nach innen wachsende Sierpinski-Dreieck wiederspricht aus solcher Sicht schlichtweg der euklidschen Geometrie. Die sich dynamisch entwickelnden inneren Dreiecke zeigen uns nämlich in Bezug der Entwicklung von Fläche und Umfang zwei gegenläufige Bewegungen: Während die Gesamtfläche der Dreiecke zunehmend gegen Null läuft, wächst deren Umfang gegen unendlich. Wir werden plötzlich mit den beiden „Endpunkten“ unserer linearen Weltsicht konfrontiert, mit dem Nichts und dem Unendlichen – und das gleichzeitig. Aus der mathematisch-geometrischen Sicht der euklidschen Geometrie, wie wir sie herkömmlich verstehen, entsteht ein Problem. Um den Sachverhalt dennoch mathematisch erfassen zu können, haben die Mathematiker eine neue Geometrie ersonnen, die sogenannte fraktale Geometrie. Mit ihr wird der Begriff der „fraktalen Dimension“ eingeführt.
Diese andere, hinzutretende Dimension fordert und eröffnet eine neue Ebene des Bewusstseins, in der zwei gegenläufige Bewegungen (Funktionen) sichtbar werden, die beide auf ihre eigene Weise diese höhere Dimension zur Anschauung bringen. Jener Umstand ist auch Gegenstand der Religion. Er hat viele Facetten. Doch wird er vor allem in der allgegenwärtigen Spannung zwischen Geist (3) und Substanz (4) wahrgenommen.
In der christlichen Tradition wird die äußere Gegenläufigkeit von zwei Funktionen, die Ausdruck ein und der gleichen Ganzheit sind, beispielsweise durch die Initiierung Jesus durch Johannes dem Täufer beschrieben (Joh 3,29). Johannes der Täufer wird mit der Taufe Jesu zur Quelle des Christentums. Die Anhänger des Johannes sprechen diesen auf die „Rivalität“ zu Jesus an, denn dieser tauft nun ebenfalls. Johannes klärt ihr Verhältnis mit den Worten: „ … er muss wachsen, und ich muss abnehmen“. Mit Johannes und Jesus erscheinen zwei äußerlich gegenläufige Bewegungen (siehe ![]() ). Sowohl Johannes als auch Jesus sind Handelnde (3). Sie beeinflussen und verändern auf ihrer Weise durch ihre von einander verschiedenen Funktionen die Welt. In ihrer Aufeinanderfolge haben sie zwar ein polares aber vor allem ein additives Verhältnis zueinander. Dabei wird ersichtlich, dass auch das abwärts gerichtete Dreieck – die abwärts gerichtete Funktion – nicht notwendiger Weise ein Vertreter des Bösen und Destruktiven ist. Das gleiche Phänomen zweier gegenläufiger Funktionen sehen wir auch in der Entwicklung der Fibonacci-Zahlen (Link setzen) oder der Entwicklung der Zahlenreihe des goldenen Schnittes (Link setzen), die jeweils durch zwei gegenläufige Funktionen entstehen. [ix]
). Sowohl Johannes als auch Jesus sind Handelnde (3). Sie beeinflussen und verändern auf ihrer Weise durch ihre von einander verschiedenen Funktionen die Welt. In ihrer Aufeinanderfolge haben sie zwar ein polares aber vor allem ein additives Verhältnis zueinander. Dabei wird ersichtlich, dass auch das abwärts gerichtete Dreieck – die abwärts gerichtete Funktion – nicht notwendiger Weise ein Vertreter des Bösen und Destruktiven ist. Das gleiche Phänomen zweier gegenläufiger Funktionen sehen wir auch in der Entwicklung der Fibonacci-Zahlen (Link setzen) oder der Entwicklung der Zahlenreihe des goldenen Schnittes (Link setzen), die jeweils durch zwei gegenläufige Funktionen entstehen. [ix]
Die symbolische Bedeutung des Sierpinski-Dreiecks liegt in der Beziehung der Dimensionen zueinander. Wir leben in einer sehr realen, konkreten Welt. Sie und all ihre manifesten Dinge werden durch den Archetyp der Vier umschrieben. Als geistige Wesen haben wir jedoch auch und vor allem Anteil an einer anderen, einer geistigen Dimension, die in den konkreten Manifestationen aufscheint. Die konkrete Welt (4) ist aus unserer Sicht umgeben von einem Geistigen (3). Ob nun dieses Geistige der Welt vorausliegt oder erst ein Produkt der manifesten Welt ist, ist ein bekannter Streitpunkt zwischen den Religionen und den Naturwissenschaften. In jedem Falle stehen die beiden Archetypen nebeneinander und solange gegeneinander, bis wir einen dritten verbindenden Punkt erkennen und wirksam werden lassen. Dieses Dritte ist das Bewusstsein (5). Es ist nach dem Vorbild des pythagoreischen Dreiecks (3-4-5) in der Lage, Geist (3) und Substanz (4) auf eine rechte Weise (rechtwinklig) miteinander zu verbinden. Bis dahin wird das Bewusstsein (5) sich seiner selbst nicht wirklich gewahr und nimmt die Spannung zwischen 3 und 4 im empfundenen Außen wahr. Dieses Bild vermittelt uns das Sierpinski-Dreieck. Seine fraktale Entwicklung weist – in der Wirkrichtung der Materie (4) gefangen – in die unendliche Tiefe.
Das Sierpinski-Dreieck berichtet uns durch seine Gestalt von den vier ersten Archetypen und ihren Beziehungen zueinander. Doch enthält es noch keine unmittelbare Zuordnung zu den natürlichen Zahlen. Das leistet erst ein anderes Dreieck, das Pascal’sche Dreieck.
3.2 Das Pascal’sche Dreieck
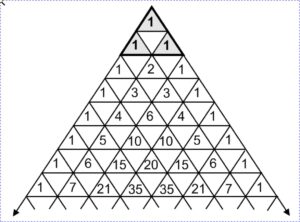 Das Pascal’sche Dreieck entsteht, wenn man initial drei Einsen in einem Dreieck anordnet. Die darunter fortlaufenden Zahlenreihen werden so gebildet, dass Anfang und Ende der Reihe stets eine Eins ist und die übrigen Zahlen jeweils die Summe der zwei darüber liegenden Zahlen sind. So entstehen nach unten wachsende Dreiecke, die von der Eins gebildet und gefasst sind und deren inneren Ausbreitungen durch das Prinzip der Addition hervorgebracht werden. Die Zahlen des Pascal’schen Dreiecks gehen aus der Dreiecksordnung systematisch hervor.
Das Pascal’sche Dreieck entsteht, wenn man initial drei Einsen in einem Dreieck anordnet. Die darunter fortlaufenden Zahlenreihen werden so gebildet, dass Anfang und Ende der Reihe stets eine Eins ist und die übrigen Zahlen jeweils die Summe der zwei darüber liegenden Zahlen sind. So entstehen nach unten wachsende Dreiecke, die von der Eins gebildet und gefasst sind und deren inneren Ausbreitungen durch das Prinzip der Addition hervorgebracht werden. Die Zahlen des Pascal’schen Dreiecks gehen aus der Dreiecksordnung systematisch hervor.
Das Pascal’sche Dreieck ist dem Mathematiker auf vielfältige Weise nützlich. Es zeigt die unterschiedlichsten Zahlenreihen, die natürliche Reihe der Zahlen, die Reihe der Dreieckzahlen, der Viereckzahlen u.a. Wir können aus ihm sogar systematisch die Reihe der Fibonacci-Zahlen entwickeln, obwohl sie in ihm gar nicht unmittelbar vorkommt. Die Komplexität des Dreiecks und das in ihm vorhandene Erkenntnispotential sind erstaunlich. Sein Wesenskern aber bleibt uns verschlossen, weil wir das Wesen der Zahlen in ihrer Mehrdimensionalität nicht erfassen. Der Mathematiker schätzt das Dreieck vor allem, weil es ihm ermöglicht, Aufgaben der Kombinatorik zu lösen. Er kann ihm beispielsweise den sogenannten Binomialkoeffizienten entnehmen, den wir von den binomischen Formeln her kennen und der uns eine einfache mathematische Funktion beschreibt. Das Dreieck zeigt uns deutlich, wie man einen Zusammenhang, der eigentlich in der Fläche begründet ist, auf eine lineare mathematische Funktion herunterbrechen und erfassen kann.
Das Pa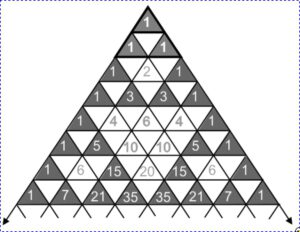 scal’sche Dreieck hat eine enge Beziehung zum Sierpinski-Dreieck. Färbt man einmal alle geraden Zahlen ein, so treten die Umrisse des Sierpinski-Musters hervor. Die Dreiecke sind miteinander verwandt. Sie haben den gleichen Hintergrund.
scal’sche Dreieck hat eine enge Beziehung zum Sierpinski-Dreieck. Färbt man einmal alle geraden Zahlen ein, so treten die Umrisse des Sierpinski-Musters hervor. Die Dreiecke sind miteinander verwandt. Sie haben den gleichen Hintergrund.
Sie haben zugleich auch ein polares Verhältnis zueinander: Die geraden Zahlen im Pascal-Dreieck entsprechen den Lücken im Sierpinski-Dreieck. Beide entstehen durch Iteration, welche eine fortlaufende geometrische Ähnlichkeit hervorbringt. Während aber beim Sierpinski-Dreieck jedes weitere Iterationsdreieck durch die gleichen Regeln wiederum ersetzt wird und sich so das Gesamtbild unendlich in seine Tiefe hinein entfaltet, entfaltet sich das Pascal’sche Dreieck nach außen – in die Ebene hinein – indem es nach unten unendlich wächst.
Das iterativ erzeugte Sierpinski-Dreieck bleibt in seiner flächenhaften Begrenzung erhalten. Das Pascal-Dreieck dehnt sich in der Fläche aus und sprengt endlich im Unendlichen die Fläche.
Beide Dreiecke basieren auf unendlichen Bauplänen, welche geometrisch abgebildet werden. Beide zeigen sie die Idee des Unendlichen, dargestellt an der Geometrie der Dreizahl.
3.3 Das Zahlendreieck (n. Stelzner)
Die beiden vorgestellten Dreiecke eröffnen uns einen Blick auf die natürlichen Zahlen und ihre Gestaltungskraft. Das Sierpinski-Dreieck und das Pascal’sche Dreieck zeigen uns auf polare Weise Zusammenhänge zwischen der geometrischen Dreigestalt und den originären Ordnungssymbolen, den Zahlen. Das Sierpinski-Dreieck weist uns vor allem auf die Beziehung benachbarter Dimensionen in Form der fraktalen Aufspaltung hin. Dabei lässt es eine direkte Zahlbeziehung nur bezüglich der Dreizahl (Geist) und der Vierzahl (Substanz) sichtbar werden. Das Pascal’sche Dreieck verbleibt im Gegensatz zum Sierpinski-Dreieck in seiner Dimension und entfaltet sich ins Außen. Es bildet zudem noch die kontinuierliche Reihe der Zahlen, sowie zahlreiche Varianten davon ab. Beide Dreiecke eröffnen uns einen wertvollen, aber auch einen sehr speziellen Blick auf die natürlichen Zahlen und ihre Gestaltungskraft. Sie lassen aber in Hinblick auf die Prinzipienlehre Platons keine unmittelbar sichtbaren Beziehungen zwischen den einzelnen, fortlaufenden Zahlen als Ideen erkennen.
Mit anderen Worten: Wir denken natürlicherweise in der linearen Ordnungsfolge der natürlichen Zahlen (0 – 123456 … – ∞). Die Welt aber entwickelt sich nicht linear. Sie folgt vielmehr dem Muster der Dreizahl, das im Dreieck seinen Ausdruck findet. Wir benötigen deshalb eine Verbindung unseres Ordnungsmusters (Zahlen) mit der Dynamik (3), die unsere Entwicklung vorantreibt. Gelingt es uns, diese Synthese zu erschauen, dann können wir hoffen, einen Einblick in die Qualitäten der Zahlen, in die Ideen Platons zu bekommen. Praktisch ausgeführt bedeutet das, dass wir die fortlaufenden Zahlen nicht wie gewohnt als fortlaufenden Zahlenstrahl niederschreiben, sondern sie in einem Muster von wachsenden Dreiecken abtragen.
- Die zwei Sichtweisen oder das Geist-Materie-Problem, Platon versus Aristoteles
(s.a. Aufsatz 2Platon vs Aristoteles.docx /Link setzen ???)
Keine anderen Philosophen haben unser Weltbild so nachhaltig geprägt, wie Platon und Aristoteles. Aristoteles war mehr als 20 Jahre der Schüler Platons und doch erscheint uns heute der Unterschied zwischen beiden Philosophien unüberbrückbar. Er wirkt wie eine Zensur und wurde nicht selten zum Kriterium zwischen einem idealistischen oder einem materialistischen Weltbild und damit zum Kriterium, ob das Sein das Bewusstsein bestimmt oder umgekehrt. Eine solche ausschließlich polare Sicht wirkt verhängnisvoll, denn sie verfehlt die tiefen und gemeinsamen Aussagen der beiden Philosophen.
Der Scheidepunkt zwischen der Philosophie Platons und der seines Schülers Aristoteles ist deren unterschiedliche Antwort auf die Frage nach der letzten Ursache, die Frage nach dem Konstitutionsgrund des Seins. Platon beantwortet sie mit seiner Ideen- bzw. Prinzipienlehre, also mit dem übergeordneten Begriff des „Geistes“. Aristoteles beantwortet die Frage mit dem Begriff der „Substanz“.
Unsere nur differenzierende und somit spaltende Sichtweise lässt den Unterschied unüberbrückbar erscheinen. Die Quelle liegt in unserer Unkenntnnis über die ersten vier Archetypen. Sie bilden den Logos, der Platon und Aristoteles eint. Wer sich heute mit den Ausführungen des Aristoteles ohne genaue Kenntnis der Ideenlehre und ihrer geometrischen Gleichnisse beschäftigt, der unterschätzt das, was Aristoteles 20 Jahre lang in der Akademie geprägt hat. Das ist vor allem die Kenntnis über das Wesen der Vierzahl, welche der Archetyp ist, der die Substanz schlechtweg abbildet. Die Vierzahl und Substanz verkörpert eine Urgesetzlichkeit, ein universell geltendes Additionsprinzip nach dem jegliche Manifestation durch die Wirkung der Triade zustandekommt. In der Vier werden dank der Wirkung der Drei die sich einstigen Antagonisten zu einem Ganzen verbunden und manifestiert. Das Gesetz war eine Art Urformel und galt in der Akademie als ein heiliges Gesetz, auf das der Überlieferung nach die Akademiemitglieder einen Eid schworen.
Auf seiner Grundlage entwickelt auch Aristoteles seine Ausführungen. Wendet man es auf die scheinbar kontroversen philosophischen Ausführungen von Platon und Aristoteles an, so enthüllen sie sich als zwei Seiten einer größeren Ordnung. In ihrem scheinbaren Widerspruch und Verhältnis zueinander scheint die Ordnung auf, welche man heute gemeinhin als Ontologie oder Metaphysik bezeichnet. Nach ihr ist die Substanzlehre des Aristoteles die logische und konsequente Weiterführung und Ergänzung der Lehre Platons. Mit anderen Worten: Die umfassende Kenntnis der Ideenlehre ist regelrecht die Voraussetzung, um die Lehre des Aristoteles umfassend zu verstehen und nicht der unauflösliche Widerspruch zu ihr.
Die Ideenlehre enthält die Metaphysik, welche allen Akademiemitglieder mündlich vermittelt wurde. Die sogenannte ungeschriebene Lehre ist sozusagen das Bindeglied zwischen Platon und Aristoteles und solange wir diese nicht kennen, können wir das Verhältnis der beiden Philosophen zueinander nicht angemessen beurteilen. Das gilt insbesondere für die gegenseitige Beziehung von Geist und Substanz, wie sie Platon und Aristoteles zur Grundlage ihrer Philosophien gemacht haben.
4.1 Das pythagoreische Dreieck – ein geometrisches Gleichnis
Eine vollständige und systematisch nachvollziehbare Lehre der Prinzipien wie sie in der Akademie gelehrt wurde, liegt uns nicht vor, denn sie wurde stets nur mündlich weitergegeben. Wir haben aber Kenntnis über das geistige Fundament der Akademie, das trotz der uns auffallenden Unterschiede zwischen Platon und Aristoteles als deren Minimalkonsens angesehen werden muss. Zu ihm zählen vier Grundqualitäten: (1) Einheit, (2) Polarität, (3) Geist/Bewegung und (4) Substanz/Materie.
Betrachten wir den vor unserem Auge auftauchenden Dissens zwischen Platon und Aristoteles vor dem Hintergrund der Geometrie des pythagoreischen Dreiecks der Seitenlängen 3, 4 und 5 und verstehen dessen Größen als die o.g. Archetypen, so erhellt sich die Spannung zwischen Geist (3) und Substanz (4). Das Dreieck löst sie nicht nur fruchtbringend auf, sondern demonstriert zugleich gleichnishaft deren Konstitutionsvermögen. Es illustriert die rechte Beziehung zwischen Geist (3) und Substanz (4) und wie aus ihr das Bewusstsein (5) erwächst.
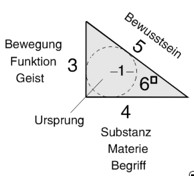
Das Gleichnis berichtet von einer triadischen Funktion, die von drei Seiten her gelesen und gedeutet werden kann, vom Geist (3), von der Substanz (4) und vom Bewusstsein (5). So erhellt es nicht nur die Konstitution des Bewusstseins als die rechte Verbindung von Geist (3) und Substanz (4) sondern auch die aktive und die passive Seite des Bewusstseins. Das Bewusstsein ist ein Dual. Wie es aus Geist und Substanz entsteht, bringt es solche auch hervor (s. Abb. 1). Sein Wesenskern und Ursprung ist die Einheit, Ganzheit und Vollkommenheit. Das pythagoreische Dreieck eröffnet uns den Blick dafür, da es dessen Symbol, den Einheitskreis umschließt und von ihm gewissermaßen gebildet wird.
Aus der moralischen Kategorie heraus informiert uns das besondere pythagoreische Dreieck darüber, dass Bewusstsein Gerechtigkeit begründet. Der Einheitskreis zielt auf den rechten Winkel, wie die Vollkommenheit auf rechtes Verhalten zielt. Das Bewusstsein visualisiert die Einheit (Einheitskreis) als ihr Zentrum. Die Gerechtigkeit schafft eine neue Qualität – eine Mitte. [x]
4.2 Die Ordnung der geometrischen Muster und die Ordnung der Philosophien
Der Inhalt geometrischer Muster erschließt sich über die Kenntnis der Archetypen. Wie die Archetypen selbst bilden auch die aus ihnen hervorgehenden Muster der Geometrie wiederum eine Ordnung ab. So ist das pythagoreische Dreieck nicht das erste der Muster. Ihm liegen der Kreis und das allgemeine, gleichseitige Dreieck voraus, die ebenfalls Gleichnisse sind. Aus dem Kreisgleichnis und dem Gleichnis des Dreiecks entsteht das Gleichnis des pythagoreischen Dreiecks, das zur Grundlage der Argumente Platons und Aristoteles wird. Es verbindet deren Prinzipien zu einem Neuen – dem Bewusstsein (5). Es hat einen dualen Charakter. Unter dessen Angesicht argumentieren Platon und Aristoteles. Sie wissen, dass sich das Bewusstsein (5) aus der Spannung und Verbindung von Geist (3) und Substanz (4) heraus konstituiert und entwickeln so nacheinander im symbolischen Abstand von 12 Jahren (!) ihre „unterschiedlichen“ Ansichten.
Dem geometrischen Gleichnis entsprechend kann man das Bewusstsein primär sowohl aus dem geistigen als auch aus dem substantiellen Ansatz heraus entwickeln. Nichts anderes haben Platon und sein Schüler Aristoteles getan. Wer jedoch die hinter ihnen wirkende Einheit und Ganzheit nicht sieht, wie sie das Gleichnis des pythagoreischen Dreiecks ausdrückt, der findet nicht zu seiner in ihm liegenden Weisheit.
Aristoteles baut auf den archetypischen Ideen Platons auf und entwickelt aus ihnen heraus Schlussfolgerungen, die im Nachhinein den Blick auf diese erweitern. Der Dissens zwischen beiden ist nur ein scheinbarer und formaler. Er ist vergleichbar mit einem heraufbeschworenen Dissens zwischen einem Erstklässler und einem Schüler, der schon fließend lesen und schreiben kann, bezüglich ihres Umganges und der Beschreibung von Buchstaben. Es ist so, als ob wir vergessen würden, dass der beste Literat noch immer die gleichen Zeichen verwendet, obwohl er sehr differenzierte und anspruchsvolle Dinge mit ihnen beschreibt. Das Tun des Literaten wertet aber die Zeichen nicht ab – im Gegenteil. Ein weiser Literat hat vielmehr großes Interesse an Nachfolgern, welche sich zunächst – wie Erstklässler – mit den grundlegenden Zeichen der Sprache „auf einfache, lineare Weise“ beschäftigen.
4.3 Aristoteles und die Konzentration auf das Objekt
Die aristotelische Philosophie entstand aus der platonischen. Das Mittel war die dialektische Methode, bei der Aristoteles zu der bestehenden These Platons vorübergehend eine Gegenthese aufbaut. Das Wesen der Methode sowie eines jeden Archetypus besteht in einer weiterführenden Beschreibung des Vorhandenen, in der das Vorhandene seinen Platz im Sinne der Triade und Synthese findet. So wird die zuvor teilweise negativ empfundene Spannung (2) fruchtbar und endlich von der Ganzheit (1) wieder eingeholt.
Aristoteles machte das, was ein besonderer Schüler immer tut, er entwickelt die Lehren des Meisters fort. Aristoteles griff die von Platon verwendeten Begriffe „idea“ und „eídos“ auf, differenzierte sie aber voneinander. Mit „idea“ bezeichnete er weiterhin das, was wir heute noch die „platonischen Ideen“ nennen, stellte ihnen aber den Begriff des „eídos“ gewissermaßen gegenüber. Unter „eídos“ verstand Aristoteles nun die „Form“ eines sinnlich wahrnehmbaren Einzeldings, die als Formursache der Materie ihre Gestalt verleiht, ihr gleichsam innewohnt und die von der Materie nicht zu trennen ist.
Die Differenzierung durch Aristoteles war notwendig, um eine seiner Ansicht nach noch unvollkommen gebliebene Vorstellung von der Substanz zu korrigieren. Damit trat er einer möglicherweise verkürzten und somit falschen Vorstellung von einer linearen Sicht auf die Ideen entgegen. Nach der Prinzipienlehre entsteht die Substanz mit der Zahl Vier. Alle Substanz ist Ausdruck der Zahl Vier. Mit ihr tritt das allgemeine Sein in das spezielle Sosein. Mit ihr beginnt die Existenz im konkreten Sinn und somit die Schöpfung. In diesem Sinne ist die Zahl 4 nicht nur etwas völlig Neues (d.h. ein neuer Beginner: 1à4) sondern auch der Urgrund der Schöpfung als solche. Dieses Muster war eine Grundvorstellung in der Akademie und einte auch Platon und Aristoteles. Die aristotelische Differenzierung zielt nun auf die der Vier „vorangehende“ Trias, die Aristoteles offenbar besser verstanden wissen will.
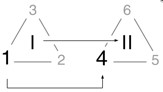
Aristoteles wendet sich mit Recht gegen die Vorstellung der „Trias“ in einem linearen Sinn, bei der man die ihr zugehörigen drei Elemente gewissermaßen (zurück-) zählend interpretiert (… 3-2-1). Er möchte die Trias als eine erste Ganzheit (Δ) stehen lassen und sie der Linearität entheben. Sie steht für das Prinzip des Ursprungs an sich (s. Abb. 2).
Die aristotelische Differenzierung verhindert, die Ideen Platons so zu interpretieren, als ob sie der Substanz zeitlich oder räumlich vorausliegen würden. Zeit und Raum entstehen erst mit dem Archetyp der Vierzahl. Man kann sie nicht, ohne einen Irrtum zu begehen, in seiner Vorstellung in die Trias zurückzutragen.
Aus solcher Erkenntnis heraus kann man nicht mehr sagen, dass die ideenhaften Urbilder „hinter“ den sinnlich wahrnehmbaren Objekten und gleichfalls außerhalb ihrer existieren. Vielmehr liegen sie in den Dingen selbst. Die Differenzierung durch Aristoteles stellt noch einmal klar, dass die Ideen nichts Trennendes und nichts von den Dingen Getrenntes sind und keine eigenständige Anderswelt repräsentieren sondern die Grundkonstitution der Existenz, die Natur der Natur („natura naturans“)[xi] beschreiben.
Die Kenntnis der Archetypen führt Aristoteles und Platon zusammen. Platon unterscheidet zwar noch zwischen den Ideen, die dem Geistigen und somit der Zahl 3 zugehören und den konkreten Formen, welche „erst“ durch die Zahl 4 erscheinen. Doch manifestiert sich jede Zahl schon in ihrem Begriff immer auch als Form. Inhalt und Form, Zahl und Erscheinung, Geist und Substanz sind in der Zahl eines. Diese Leistung erbringen zu können, zeichnet das Bewusstsein (5) aus.
In der Prinzipienlehre werden die Ideen über die Zahl Drei als reine Funktionsprinzipien begriffen. Doch treten sie über die Formen in Erscheinung, wirken in ihnen und sind von ihnen nicht zu trennen. Das weiß auch Platon. So nimmt er beispielsweise im Dialog Philebos eine Einteilung alles Seienden vor, welche konsequenterweise und explizit 4 Gattungen aufweist: (1) Das Unbegrenzte, (2) das Begrenzte, (3) die Ursache ihrer Vermischung und (4) das aus beiden sodann Gemischte.[xii]
Die scheinbare Differenz zwischen Platon und Aristoteles klärt sich an der Frage der Beziehung von Geist und Substanz, der fundamentalen Frage aller Philosophie. Kein Philosoph vermag die Frage abschließend zu klären, sofern er nicht über eine wirkliche Metaphysik verfügt, anhand derer er die Entitäten Geist und Substanz einer verbindlichen Ordnung zuführen kann. In der platonischen Akademie hat diese Aufgabe die sogenannte Prinzipienlehre übernommen.
Kennt man die Prinzipienlehre nicht, so wird man nicht nur die Ausführungen Aristoteles gegenüber Platon falsch einordnen. Man wird wegen des – im umfassenden Sinn – gewichtigen Materiebezuges den aristotelischen Ausführungen einen Vorzug geben und die Welt in ihrer Vierheit und Vielheit endlos ausdeuten, ohne die hinter ihr wirkende Drei-Einheit auf rechte Weise zu würdigen. So geschah es in der scholastischen Theologie des Mittelalters. Sie bezieht sich im wesentlichen auf Aristoteles und hat – wie beispielsweise Thomas v. Aquin – nahezu alles ausdifferenziert. Erst Nikolaus von Kus (Cusanus) [xiii] hat der ausufernden Scholastik mit dem Gedanken der „Coincidentia oppositorum“ (Gott ist der Zusammenfall der Gegensätze) einen Gegenpol gesetzt und die Dreizahl entsprechend gewürdigt. Die Einheit führte wieder Regie. Cusanus hat dem entsprechend angemahnt, dass die „höchste Wahrheit leicht zu erfassen“ und eine „gute Theologie kurz und leicht“ sei.
[i] Augustinus, De diversis quaestionibus 46.
[ii] Platon, Politeia 510c–511d
[iii] Die zugehörigen Quellen sind zu finden bei Marie-Dominique Richard: L’enseignement oral de Platon, Paris 1986, S. 243–381.
[iv] s. dazu ein Zitat aus Wikipedia:
„ … In mehreren unzweifelhaft echten Dialogen artikuliert Platon seine Skepsis gegenüber der Schrift als Medium des Wissenstransfers und bringt seine Bevorzugung mündlicher Wissensvermittlung zum Ausdruck. Eine ausführliche Erläuterung seiner Position bietet er im Dialog Phaidros. Dort begründet er die Überlegenheit mündlicher gegenüber schriftlicher Verbreitung philosophischer Lehren mit der weitaus größeren Flexibilität des mündlichen Diskurses, die ein entscheidender Vorteil sei. Der Autor eines Textes könne sich nicht auf den Kenntnisstand und die Bedürfnisse der einzelnen Leser einstellen, er könne weder deren Fragen beantworten noch auf Kritik eingehen. All dies sei nur im Gespräch möglich; dort sei die Sprache lebendig und beseelt. Das Geschriebene sei nur ein Abbild des Gesprochenen. Das Schreiben und Lesen führe nicht nur zu einer Schwächung des Gedächtnisses, sondern sei auch zur Vermittlung von Weisheit ungeeignet; diese könne nur durch mündlichen Unterricht erfolgen. Nützlich seien geschriebene Worte nur als Gedächtnisstütze für diejenigen, die schon Bescheid wissen. Literarische Tätigkeit sei nur Spielerei. Das Wesentliche seien die persönlichen Gespräche mit Schülern, bei denen die Worte auf jeweils individuelle Weise in die Seele geschrieben würden. Nur wer so lehren könne, sei als Philosoph zu betrachten. Wer hingegen nichts „Wertvolleres“ (timiōtera) habe als schriftliche Texte, an deren Formulierung er lange gefeilt hat, der sei nur Schriftsteller. Das „Wertvollere“ – die Deutung dieser Stelle ist sehr umstritten – wird als Hinweis auf die ungeschriebene Lehre gedeutet.“
[v] Plato, Der Staat, Siebtes Buch, 525St.
Was denn Zahlenkunst ist, das legt Platon u.a. wie folgt dar:
„ … was denn jeder mit als Erstes erlernen muss. Diese ganz bescheidene Weisheit: die richtige Kenntnis der Eins, der Zwei und der Drei“ (Plato, Der Staat, Siebtes Buch, 522 St.). Dass unter der »richtigen« Kenntnis nicht nur eine quantitative sondern vor allem auch eine der übergeordneten Idee zugehörige qualitative Schau zu verstehen ist, das stellt Platon deutlich heraus: „Es obliegt uns also dies Fach (Zahlenkunst) zum gesetzlichen Lehrfach zu machen und diejenigen, die künftig im Staate der höchsten Amtsgewalt teilhaftig sein sollen, zu veranlassen sich der Zahlenkunst zuzuwenden und sich mit ihr zu befassen nicht etwa bloß in laienhafter Weise, sondern bis sie durch reine Vernunfttätigkeit zur Anschauung der wahren Natur der Zahlen gelangt sind, eine Art der Behandlung, die nichts gemein hat mit Kaufen und Verkaufen wie bei Kaufleuten und Krämern…“. Für Platon war jenes Lehrfach ein „besonders feines Fach“, weil es, wie er es ausdrückte, „die Seele offenbar nötigt auf dem Wege des reinen Denkens sich der reinen Wahrheit zu nähern“ (Plato, Der Staat, Siebtes Buch, 525St.).
[vi] grch. εἶδος bedeutet Ansehen oder Gestalt.
[vii] „ Und jetzt, da das auf die Zahlenkunst bezügliche Lehrfach besprochen worden ist, wird mir auch klar, was für ein besonders feines Fach es ist und von wie vielfältigem Nutzen für Erreichung unseres obersten Zieles, sofern man es zur Erweiterung des Wissens, nicht aber zu Zwecken der Krämerei betreibt.“
„Siehst Du also, mein Freund, daß wir dieses Lehrfach mit vollem Recht für notwendig für uns erklären, da es die Seele offenbar nötigt auf dem Wege des reinen Denkens sich der reinen Wahrheit zu nähern?“ S. 285 f
„Ihre Ausdrücke (die der Geometrie nur scheinbar Kundigen) sind höchst lächerlich und gezwungen; denn als ob sie etwas ins Werk setzen und ihre Ausdrücke als da sind quadrieren, oblongieren, addieren und was sie sonst noch alles für Worte im Munde führen; tatsächlich aber ist der eigentliche Zweck dieser ganzen Wissenschaft nichts anderes als die reine Erkenntnis.“ S. 288
Im Dialog über den idealen Staat belehrt Sokrates Glaukon „ So läge denn mein Trefflicher, in ihr (der Geometrie) eine Kraft, die die Seele nach der Wahrheit hinzieht und philosophische Denkart erzeugt insofern, als wir dann nach oben richten, was wir jetzt verkehrterweise nach unten richten.“
[viii] „Nun aber ist die dialektische Methode die einzige, die , mit bloßen Voraussetzungen aufräumend, zum Anfang selbst vordringt, um diesen völlig sicher zu stellen; sie zieht das in Wahrheit in einem wahren Brei von Barberei vergrabene Auge der Seele mit sanftem Druck ans Licht hervor und führt es aufwärts, wobei sie sich der genannten Künste (Zahlenkunst, Geometrie und Lehre der dreidimensionalen Körper – Anm. des Verf.) als Mithelferinnen und Mitarbeiterinnen am Werke der Seelenumwendung bedient. Platons Staat, S. 298.
[ix] Leben existiert, weil wir stets in zwei Ebenen zu Hause sind, in denen unterschiedliche „Rezepte“ funktionieren: (später löschen, da zu profan?)
Wenn ihnen ein Arzt ein Rezept zum Abnehmen gibt, dann händigt er ihnen nicht etwa Kochrezept für eine Sahnetorte aus – im Gegenteil. Er gibt ihnen etwas anderes als was ein Sahne-Lüstling im allgemeinen unter einem Rezept versteht. Der Arzt und der Patient leben aus verschiedenen Ebenen/Welten heraus. Der Patient lebt in der Schlemmerwelt, die ihm inzwischen nicht mehr den erhofften Genuss zeitigt und der Arzt ist ein Wissender aus der Welt der Wissenschaften und Prinzipien, der die Menschen in der Schlemmerwelt berät. Was beide vereint, das ist die Absicht, abzunehmen.
Mit den Parametern der Schlemmerwelt, wie leckeren Diäten, Eiweißtrunks oder Trennkost werden Sie keinen dauerhaften, wirklichen Erfolg erzielen. Was nötig ist, das ist der Einbruch einer höheren Welt in die niedere, der geistigen Welt in die Schlemmerwelt. Die höhere Welt nimmt zu, die niedere ab. Beide Bewegungen, Zu- und Abnahme gehören aber dem gemeinsamen, höheren Bewusstsein an. Beide Bewegungen sind unter den Menschen anzutreffen, welche dem höheren Bewusstsein zum Durchbruch verhelfen wollen.
Vor der weitern theologischen Betrachtung, hier die praktische Konsequenz für die, welche abnehmen wollen: Ohne den Geist aus der neuen höheren Ebene, geht es nicht! Wer abnehmen will, der muss ein geistiges Ziel haben … kein körperliches. Dann aber kommt er seinem körperlichen Anliegen näher.
Wer diese neue, geistige Ebene nicht aufnimmt, der wird die „gewünschte Größe“ nicht erreichen. Wenn ein Arzt beispielsweise sagt, dass Sie bei Ihrem Gewicht eine Größe von 2,30 m haben müssten, dann können Sie essen, soviel sie wollen, Sie werden diese Größe nicht erreichen.
[x] s. Aristoteles: „Und deshalb gilt die Gerechtigkeit als oberster unter den Vorzügen des Charakters, und ‚weder Abend- noch Morgenstern sind so wundervoll.’ Und im Sprichwort heißt es: ‚In der Gerechtigkeit ist jeglicher Vorzug beschlossen.“ – 1129b
„Die Gerechtigkeit ist also eine Mitte, freilich nicht auf dieselbe Art wie die übrigen Tugenden, sondern weil sie die Mitte schafft. Die Ungerechtigkeit dagegen schafft die Extreme.“ – 1133b32
[xi] Der Begriff der „natura naturans“ geht auf Baruch Spinoza zurück. Er bezeichnet so die eine göttliche, schöpferische Substanz, welche sich in unendlich unterschiedlichen Weisen als deren Erscheinungen, den „natura naturata“ ausdrückt (s. Abb. 2). In seinem wohl bedeutendsten und wirkmächtigen Werk, der „Ethica, ordine geometrico demonstrata“ (Die Ethik mit geometrischer Methode begründet) wird deutlich, dass sich der große Zusammenhang „more geometrico“ (nach geometrischer Weise) erschließt.
Für Spinoza ist Gott (1) in allem Seienden (4) vorhanden (s. Abb. 2). Auch für ihn steht die Substanz am Anfang allen Seins. Nach Spinoza erfolgt alles notwendigerweise aus der göttlichen Natur, „auf die selbe Weise, wie aus der Natur des Dreiecks von Ewigkeit und in Ewigkeit folgt, dass seine drei Winkel gleich zwei rechten sind“. (Baruch de Spinoza: Die Ethik nach geometrischer Methode dargestellt. Band I, 1976, Prop. 17, Anmerkung, S. 23.)
Wie Descartes geht Spinoza von dem polaren Gegensatz von Geist und Materie aus. Er sah dennoch in ihnen nicht zwei gegensätzliche Substanzen, wie Descartes vor ihm (Dualismus) sondern eine einzige mit zwei Attributen (Monismus). Insofern findet der Gegensatz von Platon und Aristoteles bei Descartes und Spinoza einen Widerhall.
[xii] Platon, Philebos 23b–27c
[xiii] Cusanus übernahm nicht einfach die Lehren der Kirchen sondern suchte deren Wurzeln und fand sie in der Weisheit der Zahlen:
„Hieraus findest du, bei genauem Zusehen, daß die Vielheit der Dinge nichts anderes als eine Art und Weise des Anschauens des göttlichen Geistes ist. So schließe ich, daß man unwiderleglich sagen kann, das erste Exemplar der Dinge in der Seele des Schöpfers sei die Zahl. Das zeigt die Ergötzung und die Schönheit, die allen Dingen innewohnt und die in der Proportion besteht, die Proportion wieder in der Zahl; daher ist die Zahl der trefflichste Pfad, welcher zur „Weisheit emporführt.“
(zitiert aus „Liber de mente“, in der Übersetzung von E. Cassirer in „Individuum und Kosmos in der Philosophie der Renaissance“, Leipzig 1927)
Cusanus lehnte es ab Ordensmitglied noch Lehrer an einer Hochschule zu sein. Statt der Weltflucht in einem Ordensleben wählte er die Weltgestaltung durch ein aktives politisches Leben. Dennoch war er Kleriker und reiste beispielsweise im Dienst einer geplanten Kirchenreform für den Papst durch die Landen. Er wurde in Brixen Bischof, später Generalvikar, unter Pius II. Kardinal und stand sogar zur Papstwahl.